From Scratch: Music Theory Lesson 3 — The Math Behind Classical Sheet Music

Exploring Equal Temperament

During the Baroque period, as polyphonic music advanced, composers increasingly needed to shift between different keys. However, older systems like Pythagorean tuning and Just Intonation posed limitations when modulating. These systems, though acoustically pure in some intervals, created problems when used across a wider key range.

To resolve this, Johann Sebastian Bach embraced a more versatile system: well temperament. He titled his iconic collection The Well-Tempered Clavier—not “equal temperament” as often mistranslated, but rather a system that made all keys usable without significant tonal imbalance.

In this tuning system, the notes were adjusted slightly so that intervals became evenly distributed across all keys. While no single interval remained perfectly pure, the tradeoff allowed composers much more freedom to explore harmonically distant tonal centers—an essential development for the emergence of classical sheet music as we know it today.

Eventually, Western music evolved from well temperament to true equal temperament. In this system, the octave is divided into twelve equal parts using the twelfth root of two as the multiplier between each adjacent pitch. This mathematical approach gave birth to the twelve-tone system that underlies most modern piano notes and repertoire.

Interestingly, the equal temperament concept was independently calculated in 16th-century China by Zhu Zaiyu, though it never became widely adopted there.

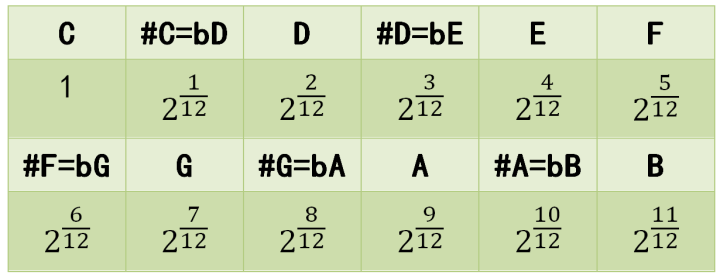
To visualize this, consider that each key on a piano has a specific frequency based on the standard pitch of A = 440 Hz. By repeatedly multiplying this by the twelfth root of two, you can determine the exact frequency of any note in the equal temperament system, such as Middle C.

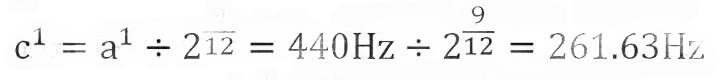
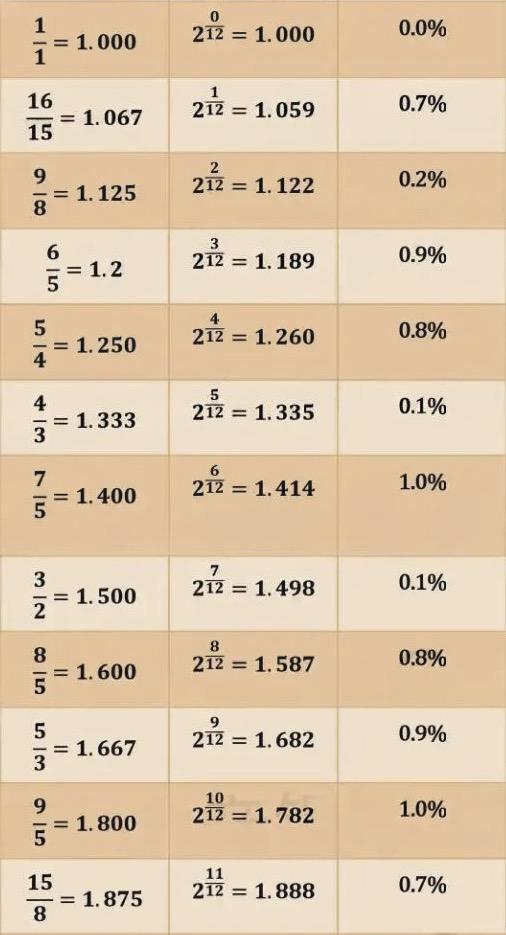
While the differences between equal temperament and other systems are subtle in terms of numerical ratios, they make a big difference in practice—especially for music students learning from piano online lessons or transposing pieces across different keys using easy sheet music.

This tuning system laid the foundation for centuries of composition—from Bach through Beethoven to Ravel and beyond. Without it, many of the pieces now studied through classical sheet music would simply not have been possible.

Equal temperament is a fascinating example of where mathematics meets art. Although other tuning systems existed—like China’s 60-tone division or India’s 22-tone system—none offered the same level of harmonic versatility and mathematical balance.

Common Questions about Tuning and Playing

Q1: How are consonance and dissonance defined in equal temperament?
A: Strictly speaking, all intervals except the octave are slightly dissonant in equal temperament, because they deviate from their pure ratios. Our current labels of “consonant” and “dissonant” are inherited from Just Intonation.

Q2: Do I need to learn tuning to play piano?
A: No, tuning is generally done by a professional technician. However, understanding tuning systems can deepen your musical interpretation and sharpen your listening skills in piano online lessons.

Q3: Why study tuning if I don’t need to do it myself?
A: Tuning systems reveal much about music history and composers’ preferences. For instance, understanding enharmonic equivalents can prevent confusion—C♯ and D♭ may share a key on the piano, but they’re not treated the same in music theory. This knowledge can also make learning from easy sheet music more meaningful.